простые графы.
В этом разделе курса мы рассматриваем понятие графа. В последнее время теория графов стала простым, доступным и мощным средством решения вопросов, относящихся к широкому кругу проблем. Это проблемы проектирования интегральных схем и схем управления, исследования автоматов, логических цепей, блок-схем программ, экономики и статистики, химии и биологии, теории расписаний и дискретной оптимизации.
определения, данные в разделе ``алгебраические системы''.
В дальнейшем, если это явно не оговаривается, мы будем рассматривать только
простые графы.
Рассмотрим различные способы задания для одного и того же графа.
В дальнейшем мы будем опираться именно на второе определение графа.
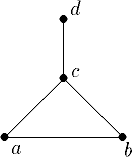
3. Матрица смежности
| a | b | c | d | |
|---|---|---|---|---|
| a | 0 | 1 | 1 | 0 |
| b | 1 | 0 | 1 | 0 |
| c | 1 | 1 | 0 | 1 |
| d | 0 | 0 | 1 | 0 |
4. Матрица инцидентности
| u | v | w | x | |
|---|---|---|---|---|
| a | 1 | 0 | 0 | 0 |
| b | 1 | 1 | 1 | 0 |
| c | 0 | 1 | 0 | 1 |
| d | 0 | 0 | 1 | 1 |
Понятие изоморфизма для графов имеет наглядное толкование. Представим рёбра графов эластичными нитями, связывающими узлы – вершины. Тогда, изоморфизм можно представить как перемещение узлов и растяжение нитей.
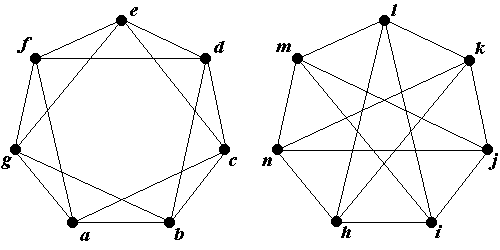
Пример 1 (изоморфизм). Покажем, что следующие два графа изоморфны.
Действительно, отображение a ® e, b ® f, c ® g, d ® h, являющееся изоморфизмом легко представить как модификацию первого графа, передвигающую вершину d в центр рисунка.
1.1 Постройте изоморфизм графов
Определение 1 (Степень вершины).
Степенью вершины назовём удвоенное количество петель, инцидентных этой вершине плюс количество остальных инцидентных ей рёбер.
1.2 Докажите, что изоморфизм сохраняет степени вершин графа. Иначе говоря, степень образа вершины при изоморфизме совпадает со степенью самой вершины.
1.3 Проверьте, изоморфны ли графы. см. Указания
1.4 Докажите, что сумма всех степеней вершин графа равна удвоенному количеству рёбер.
1.5 Докажите, что в любом графе количество вершин нечётной степени – чётное число. см. Указания
Определение 2 (Подграф). Подграфом графа называется граф, являющийся подмоделью исходного графа. Иначе говоря, подграф содержит некоторые вершины исходного графа и некоторые рёбра (только те, оба конца которых входят в подграф).
Определение 3 (Подграф, порождённый множеством вершин).
Подграфом, порождённым множеством вершин U называется подграф, множество вершин которого – U, содержащий те и только те рёбра, оба конца которых входят в U.
Определение 4 (Остовной подграф). Подграф называется остовным подграфом, если множество его вершин совпадает с множеством вершин самого графа.
Два последних определения дают два вида максимальности подграфов: максимальность множества вершин и максимальность множества рёбер. Это подтверждают следующие три задачи:
1.6 Докажите, что подграф H графа G является порождённым множеством своих вершин тогда и только тогда, когда не существует ни одного другого подграфа графа G, для которого H являлся бы остовным подграфом.
см. Решение1.7 Докажите, что подграф H графа G является остовным тогда и только тогда, когда не существует ни одного другого подграфа графа G, для которого H являлся бы подграфом, порождённым множеством своих вершин.
1.8 Докажите, что если подграф является остовным подграфом и подграфом, порождённым множеством своих вершин одновременно, то этот подграф – сам граф.
Определение 5 (Пустой, полный графы). Пустым называется граф без рёбер. Полным называется граф, в котором каждые две вершины смежны.
1.9 Докажите, что граф является пустым тогда и только тогда, когда все его подграфы – тоже пустые.
1.10 Докажите, что граф является полным тогда и только тогда, когда все его подграфы, порождённые некоторым множеством вершин – тоже полные.
1.11 Докажите, что полные (пустые) графы изоморфны тогда и только тогда, когда они имеют одинаковое количество вершин.
1.12 Докажите, что пустой граф с n вершинами содержит ровно n попарно неизоморфных подграфов.
1.13 Докажите, что граф с n вершинами является пустым тогда и только тогда, когда он содержит ровно n попарно неизоморфных подграфов.
1.14 Докажите, что полный граф с n вершинами содержит ровно n попарно неизоморфных подграфов, порождённых некоторыми множествами вершин.
1.15 Докажите, что граф с n вершинами является полным или пустым тогда и только тогда, когда он содержит ровно n попарно неизоморфных подграфов, порождённых некоторыми множествами вершин.
Определение 6 (Маршрут). Маршрутом в графе G = <V,E; I> называется последовательность вершин и рёбер вида v0,e1,v1,e2, ..., vn-1,en,vn, где vi О V, i О [0,n], ei О E, (vi-1,ei), (vi,ei) О I, i О [1,n]. Вершины v0, vn называются связанными данным маршрутом (или просто связанными). Вершину v0 называют началом, а vn – концом маршрута. Если v0 = vn, то маршрут называют замкнутым. Число n называется длиной маршрута.
Определение 7 (Цепь, простая цепь, цикл). Маршрут, в котором все рёбра попарно различны, называется цепью. Замкнутый маршрут, являющийся цепью, называется циклом. Маршрут, в котором все вершины попарно различны, называется простой цепью. Цикл, в котором все вершины, кроме первой и последней, попарно различны, называется простым циклом.
Пример 2 (цепь). Маршрут a,{a,b},b,{b,c},c,{c,a},a,{a,d},d в первом графе из примера 1 является цепью, но не является простой цепью.
Замечание. Мы будем отождествлять циклы, являющиеся циклическими перестановками друг друга.
2.1 Докажите, что изоморфизм сохраняет циклы графа.
2.2 Вернитесь к задаче 1.3 и получите для неё более простое решение. см. Указания
Графы часто используют для изображения различных отношений
(например, иерархических отношений, т.е., на языке математики –
отношений частичного порядка).
Правда, для точного представления таких графов необходимо выразить
понятие направления на графе. Мы не будем сейчас вводить новые
понятия, а будем просто использовать расположение вершин на рисунках
(одна выше или ниже другой).
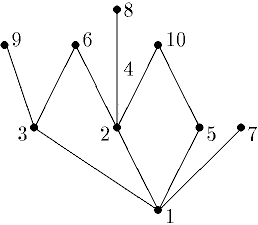
Пример 3 (граф отношения делимости). Построим граф, изображающее отношение делимости на множестве {1,2,3,4,5,6,7,8,9,10}. Принцип такой: если от одного числа до другого есть цепь, ведущая вверх, тогда второе число делится на первое.
Определение 8 (Связность). Граф называется связным, если любая пара его вершин связана.
2.3 Покажите, что отношение связанности вершин является отношением эквивалентности. см. Указания
Определение 9 (Связные компоненты). Связными компонентами графа называются подграфы данного графа, вершины которых являются классами эквивалентности отношения свзанности в данном графе.
2.4 Докажите, что связная компонента является связным графом.
Определение 10 (Цикломатическое число). Цикломатическим числом графа называется число связных компонент графа плюс число рёбер минус число вершин.
Определение 11 (Эйлеров цикл). Эйлеровым называется цикл, проходящий по каждому ребру графа ровно один раз. Граф, имеющий эйлеров цикл, тоже будем называть эйлеровым.
Пример 4 (эйлеров цикл). Построим эйлеров цикл для второго графа из задачи 1.1. Это h, {h,l}, l, {l,i}, i, {i,m}, m, {m,j}, j, {j,n}, n, {n,k}, k, {k,h}, h, {h,i}, i, {i,j}, j, {j,k}, k, {k,l}, l, {l,m}, m, {m,n}, n, {n,h}, h.
Теорема 1 (Критерий эйлеровости графа). Связный граф является эйлеровым тогда и только тогда, когда степени всех его вершин – чётные числа.
Требование связности в теореме естественно – несвязный граф может быть эйлеровым только в том случае, если только одна связная компонента содержит рёбра.*
2.5 Какие из графов, упоминающихся в задачах и примерах являются эйлеровыми ?
Кроме понятия эйлерова цикла в задачах часто возникает необходимость нахождения цепи, проходящей по каждому ребру ровно один раз (снимается требование замкнутости. Такие цепи будем называть эйлеровыми цепями.
2.6 Докажите, что в связном графе существует эйлерова цепь тогда и только тогда, когда граф содержит не более двух вершин нечётной степени. см. Указания
Определение 12 (Гамильтонов цикл). Гамильтоновым называется цикл, проходящий по каждой вершине графа ровно один раз.
2.7 Все ли графы, упоминающиеся в задачах и примерах содержат гамильтонов цикл ?
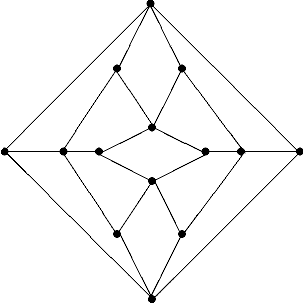
2.8 Содержит ли гамильтонов цикл граф ромбического додекаэдра:
Определение 13 (Дерево). Связный граф без циклов называется деревом.
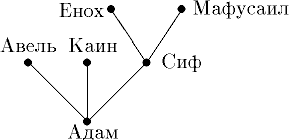
Деревья особенно часто возникают на практике при изображении различных иерархий. Например, популярны генеологические деревья.
Пример 5 (генеологическое дерево). На рисунке показано библейское генеологическое дерево.
2.9 Докажите, что граф является деревом тогда и только тогда, когда любая пара различных вершин соединена единственной цепью.
2.10 Докажите, что граф является деревом тогда и только тогда, когда он связен, но после удаления любого ребра становится несвязным.
2.11 Докажите, что количество рёбер дерева на единицу меньше количества вершин. см. Указания
Определение 14 (Лес, листья). Граф без циклов называется лесом. Вершины степени 1 в дереве называются листьями.
2.12 Докажите, что связными компонентами леса являются деревья.
2.13 Докажите, что цикломатическое число леса равно нулю. см. Указания
Деревья – очень удобный инструмент представления информации самого разного вида. Деревья отличаются общего случая от простых графов тем, что при обходе дерева невозможны циклы. Это делает графы очень удобной формой организации данных для различных алгоритмов. Таким образом, понятие дерева активно используется в информатике и программировании.
2.14 Найдите количество остовных подграфов, являющихся деревьями, в полных подграфах с 3-мя, 4-мя, 5-ю, 6-ю вершинами. см. Указания
Определение 15 (Раскраска). Раскраской графа G = (V,E) называется отображение c: V ® N . *
Определение 16 (Правильная раскраска). Раскраска называется правильной, если образы любых двух смежных вершин различны: c(u) № c(v), если (u,v) О I. Хроматическим числом графа называется минимальное количество красок, необходимое для правильной раскраски графа.
Пример 6 (раскраска). На следующем рисунке показана правильная раскраска.
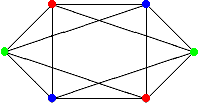
3.1 Найдите хроматические числа графов, упоминающихся в задачах и примерах.
3.2 Докажите, что если в графе все циклы имеют чётную длину, то существует правильная раскраска этого графа в 2 краски.
3.3 Докажите, что для любого дерева хроматическое число не превосходит 2.
3.4 Покажите, что необходимым условием существования гамильтонова цикла в графе с хроматическим числом равным 2 является равенство количества вершин, раскрашенных в разные краски.
3.5 Вернитесь к задаче 2.8 (о ромбическом додекаэдре) и получите её решение исходя из предыдущей задачи.
Помимо использования в дискретной математике, графы находят применение и в непрерывной математике, особенно в топологии. При этом графы представляют геометрические объекты на некоторой поверхности (часто на плоскости или на поверхности сферы.)
Определение 17 (Плоский граф). Существует правило изображение графов на поверхности: рёбра графа должны пересекаться только своими концами, то есть в точках, представляющих вершины графа.
Для графа, который может быть изображён подобным образом на плоскости, существует название: плоский граф.
Определение 18 (Грань графа). Гранью графа, изображенного на некоторой поверхности, называется часть поверхности, ограниченная рёбрами графа.
Данное понятие грани, по-существу, совпадает с понятием грани многогранника. В качестве поверхности в этом случае выступает поверхность многогранника. Если многогранник выпуклый, его можно изобразить на плоскости, сохранив все грани. Это можно наглядно представить следующим образом: одну из граней многогранника растягиваем, а сам многогранник ``расплющиваем'' так,
