Если в прошлых веках и в начале XX века алгебра изучала весьма ограниченное число алгебраических структур, то сейчас можно дать очень общее определение алгебры – а именно: наука о свойствах множеств, на которых определена та или иная система операций и отношений. В развитие такого взгляда на алгебру внес большой вклад А.И. Мальцев. В частности, он ввел понятие алгебраической системы, что и является темой данного раздела. Благодаря работам А.И. Мальцева стало ясно, что алгебра и математическая логика – две тесно связанные между собой дисциплины.
Определение 1 (Отношение). n-арным (n-местным) отношением на множестве A называется подмножество n-ой декартовой степени An множества A.
Определение 2 (Алгебраическая операция). n-арной (n-местной) алгебраической операцией (или просто операцией), определенной на множестве A называется n-местная функция f: An ® A.
Число n для n-арной операции f (n-арного отношения r) называется арностью операции f (отношения r) и обозначается n(f) (n(r)). Арности отношений – это числа большие нуля. Арности операций – это числа большие или равные нулю. Операции арности 0 представляют собой функции с областью определения, состоящей из одного элемента (n-ки длины 0) и отождествляются со значением функции.*
Для унарных операций мы будем использовать префиксную и постфиксную нотацию, а для бинарных – как правило инфиксную.
Если множество A конечно, алгебраическую операцию на этом множестве можно определить в виде таблицы. Если операция бинарная, то такое определение особенно удобно.
Пример 1 (таблица операции).
Составим таблицу
операции (+ mod 5) на множестве
{0, 1, 2, 3, 4}
| (+ mod 5) | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| 0 | 0 | 1 | 2 | 3 | 4 |
| 1 | 1 | 2 | 3 | 4 | 0 |
| 2 | 2 | 3 | 4 | 0 | 1 |
| 3 | 3 | 4 | 0 | 1 | 2 |
| 4 | 4 | 0 | 1 | 2 | 3 |
Кроме того, что таблица даёт определение операции, она наглядно выражает некоторые свойства операции. В частности, коммутативность операции соответствует симметричности таблицы относительно главной диагонали.
Определение 3 (Алгебраическая система). Алгебраической системой <A;WF;WR> называется объект, состоящий из трёх множеств: непустого множества A, множества алгебраических операций WF, определёных на A, и множества отношений WR, определёных на A. Множество A называется носителем алгебраической системы. Если алгебраическая система не содержит операций, она называется моделью, если не содержит отношений, то – алгеброй.
Символы алгебраических операций и отношений (каждый из которых имеет определённую арность) составляют сигнатуру алгебраической системы.
Мы будем иметь дело с алгебраическими системами, содержащими конечное число операций и отношений. Алгебраические системы мы будем записывать в виде: <A;f1,...,fk;r1,...,rl> , где {f1,...,fk} = WF, {r1,...,rl} = WR.
Определение 4 (Тип алгебраической системы). Типом алгебраической системы <A;f1,...,fk;r1,...,rl> называется пара наборов (n(f1),...,n(fk)) и (n(r1),...,n(rl)), состоящих из арностей операций и отношений. Тип будем записывать в виде <n(f1),...,n(fk); n(r1),...,n(rl)> .
Пример 2 (алгебраическая система).
<N ;+,·;<> является алгебраической системой типа <2, 2; 2>, так как операции +,· определены для любых двух натуральных чисел и результат снова является натуральным числом. <N;+,-;<> не является алгебраической системой, так как результат операции -, применённой к натуральным числам – не всегда натуральное число.
Задача 1. Является ли <N;+,-;Ј> алгебраической системой ?
Стандартный алгебраический подход к рассмотрению алгебраических систем – отвлечение от свойств отдельных элементов носителя, не связанных с операциями и отношениями системы, как и от способов определения (вычисления) операций и отношений, и рассмотрение только их свойств в рамках алгебраической системы. Для обозначения совпадения свойств носителей, операций и отношений в рамках самих алгебраических систем используется понятие изоморфизма.
Определение 5 (Гомоморфизм). Пусть A = <A;f1,...,fk;r1,...,rl> и B = <B;g1,...,gk;p1,...,pl> – алгебраические системы одного типа <m1,...,mk; n1,...,nl>. Отображение j:A ® B называется гомоморфизмом алгебраической системы A в B, если выполняются следующие условия:
Пример 3 (гомоморфизм).
Любое отображение любой модели <A;p> типа <2> на модель <A;V> (где V – пустое бинарное отношение) является гомоморфизмом, так как первое условие выполняется ввиду отсутствия операций, а второе – из-за того, что посылка импликации всегда ложна.
Определение 6 (Изоморфизм). Если гомоморфизм является биекцией и обратное отображение тоже – гомоморфизм, то такой гомоморфизм называется изоморфизмом. Алгебраические системы, для которых существует изоморфизм, называются изоморфными.
Иначе говоря, изоморфизм алгебраических систем A = <A;f1,...,fk; r1,...,rl> и B = <B;g1,...,gk;p1,...,pl> одного типа <m1,...,mk; n1,...,nl> – это взаимно-однозначное отображение j множества A на B, такое что выполняются условия:
Для алгебр условие 2 автоматически выполняется, поэтому для алгебр изоморфизмы – это гомоморфизмы, являющиеся биекцией.
Покажем, что алгебры <R ; +> и <R+ ;·> * изоморфны. Определим отображение j : R ® R+ как j(x) = ex. Это отображение – биекция и j(x+y) = e(x+y) = ex · ey = j(x) · j(y).
Пример 5 (изоморфизм моделей).
Покажем, что модели <R; Ј> и <R; і> изоморфны. Определим отображение j(x) = -x. Это отображение – биекция и j(x) і j(y) Ы -x і -y Ы x Ј y.
Определение 7 (Автоморфизм). Изоморфизм алгебраической системы на себя называется автоморфизмом. Автоморфизм, являющийся тождественным отображением называется тривиальным.
Задача 2. Доказать, что алгебры <Q ; + >* и <Z ; + >* неизоморфны.
Задача 3. Найти количество автоморфизмов модели <{2,3,4,5,6,7}; r>, где r – отношение взаимной непростоты*.
Определение 8 (Подсистема). Подсистемой алгебраической системы <A;WF;WR> называется алгебраическая система <A';WF';WR'>, в которой A' Н A, значения всех операций из WF' на A' совпадают со значениями операций из WF и отношения из WR' на A' совпадают с отношениями из WR. При этом подмножество A' называется замкнутым в системе <A;WF;WR>.
Заметим, что гомоморные образы алгебр всегда изоморфны подалгебрам, но гомоморные образы моделей – не обязательно изоморфны подмоделям данной модели.
Пример 6 (гомоморные образы модели).
Модель <{0,1}; <> можно гомоморфно отобразить на модели <{0,1}; Ј >, <{0}; {(0,0)}> и т.д., но они не являются подмоделями исходной модели.
Теорема 1 (Пересечение подсистем). Пересечение произвольной совокупности подсистем любой алгебраической системы либо пусто, либо является подсистемой.
Пример 7 (пересечение алгебр).
Алгебры <{0, 2, 4}; (+ mod 6) > и <{0, 3}; (+ mod 6) > являются подалгебрами алгебры <{0, 1, 2, 3, 4, 5}; (+ mod 6) >. Пересечением этих алгебр будет алгебра <{0}; + > с носителем, состоящим из одного элемента - 0 и операцией, которую мы обозначили через +, так как она применима только к элементу 0 и совпадает с результатом обыкновенного сложения.
Определение 9 (Замыкание множества в алгебраической системе). Носитель минимальной алгебраической системы, содержащей множество A, называется замыканием множества A в алгебраической системе.*
Пример 8 (замыкание множества).
Замыканием множества {-1,1} в алгебре <Q; + > является множество Z целых чисел, так как <Z; + > – алгебра и, если подалгебра алгебры <Q; + > содержит -1 и 1, она содержит все целые числа.
Алгебраическая система может быть изоморфна своей подсистеме.
Пример 9 (подалгебра, изоморфная алгебре).
Покажем, что алгебры <N; +> и <{2,4,6,...}; +> изоморфны. Определим отображение j : N ® {2,4,6,...} как j(x) = 2 x. Это отображение – биекция и j(x+y) = 2 (x+y) = 2 x + 2 y = j(x) + j(y).
Определение 10 (Прямое произведение систем). Прямым произведением алгебраических систем A = <A;f1,...,fk;r1,...,rl> и B = <B;g1,...,gk;p1,...,pl> типа <m1,...,mk; n1,...,nl> называется алгебраическая система A ґ B = <A ґ B;h1,...,hk;q1,...,ql> того же типа, такая что
Прямое произведение алгебраической системы A на себя n раз называется степенью алгебраической системы A и обозначается An.
Пример 10 (прямое произведение).
Рассмотрим прямое произведение алгебраической системы A = <R; +; Ј > на себя.
Носителем алгебраической системы A2 является множество пар вещественных чисел (x,y) с операцией покоординатного сложения и отношением порядка Ј, таким что (x1,y1) Ј (x2,y2) Ы x1 Ј x2 и y1 Ј y2, то есть одна пара меньше или равна другой тогда и только тогда, когда каждая координата первой пары меньше или равна соответствующей координате второй пары.
Кроме того, рациональные (целые, целые неотрицательные, натуральные) числа со сложением и умножением тоже образуют алгебру. Действительно, сумма и произведение двух рациональных (целых, целых неотрицательных, натуральных) чисел – снова рациональное (соответственно целое, целое неотрицательное, натуральное) число. Таким образом, множества рациональных, целых, целых неотрицательных, натуральных чисел – замкнуты в <R; +, · > и <Q; +, · >, <Z; +, · >, <Z+; +, · >, <N; +, · > – алгебры, являющиеся подалгебрами <R; +, · >.
Рассмотрим все подмножества некоторого множества A (обозначим их через P(A) ). Операции объединения, пересечения двух множеств и дополнения множества X до множества A (обозначим через - X ) являются алгебраическими операциями. Действительно, они определены для любых подмножеств множества A и результат этих операций – снова подмножество множества A. Пустое множество и само множество A – тоже подмножества множества A.
Итак, алгеброй подмножеств множества A называется алгебра <P(A); И, З, -, Ж, A >.
Можно ли определить алгебру подмножеств аксиоматически ? Ответ на этот вопрос мы получим в разделе 6.
Алгебра изучает не отдельные алгебраические системы, а классы алгебраических систем. А именно те алгебраические системы, которые удовлетворяют некоторой системе аксиом. То есть изучаются в основном свойства общие для всех алгебраических систем из данного класса вместо того, чтобы изучать свойства каждой отдельно. Такой подход оказывается не только продуктивным, но и напрашивающимся (наиболее ``естественным''). Часто для классов алгебраических систем рассматриваются более узкие классы, получающиеся добавлением новых аксиом.
В следующих разделах мы рассмотрим следующие классы алгебраических систем: частично-упорядоченные множества, решетки, булевы алгебры, графы, группы и полугруппы.
Определение 11 (Граф). Графом называется двуосновная модель <V, E; i >, где i – бинарное отношение множеств V и E, такое, что каждый элемент e О E находится в отношении i либо ровно с одним, либо ровно с двумя элементами множества V.
При этом элементы множества V называются вершинами графа, элементы множества E называются рёбрами графа, а отношение i – отношением инцидентности. Вершины, инцидентные одному и тому же ребру, называются смежными.
Графы обычно изображаются в виде геометрических фигур, так что вершины графа изображаются точками, а ребра – линиями, соединяющими те точки, соответствующим вершинам которых ребра инцидентны.
Определение 12 (Петли, кратные рёбра). Если ребро инцидентно только одной вершине, его называют петлей. Рёбра называются кратными, если они инцидентны одним и тем же вершинам.
Граф без кратных рёбер можно определить как модель <V; c >, где c – бинарное отношение (отношение смежности).
Предложение 1. Для любых двух графов G1 = <V1, E1; i1 > и G2 = <V2, E2; i2 > без кратных рёбер справедливо следующее: если модели <V1; c1 > и <V2; c2 > (где c1 (c2) – отношение смежности вершин в графе G1 (соответственно G2)) изоморфны, то и сами графы G1 и G2 изоморфны.
Определение 13 (Простой граф). Граф без кратных рёбер и петель называется простым графом.
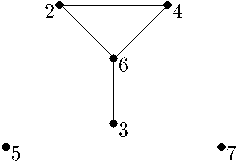
Пример 11 (граф).
Рассмотрим модель из задачи 3 как граф. Чтобы не загромождать изображение, удалим из него все петли.

Если этот граф изобразить в пространстве*, то каждому автоморфизму модели из задачи 3 будет соответствовать симметрия полученной геометрической фигуры.
Определение 14 (Частично-упорядоченное множество).
Частично-упорядоченным множеством называется модель
<A; Ј > ,
бинарное отношение Ј которой удовлетворяет системе аксиом:
Определение 15 (Решёточно-упорядоченное множество).
Частично-упорядоченное множество <A; Ј >
называется решёточноупорядоченным, если
для любых двух элементов a, b О A существует точная нижняя
грань inf(a,b) О A и точная верхняя грань
sup(a,b) О A.
Определение 16 (Решётка). Решёткой называется алгебра <A; Ъ, Щ > , операции Ъ, Щ которой удовлетворяют следующей системе аксиом:
Теорема 2 (Связь ч.у.м. и решеток). Если алгебра <A; Ъ, Щ > является решёткой, то модель <A; Ј >, где отношение Ј определено следующим образом: x Ј y Ы x Щ y = x – решёточно-упорядоченное множество.
Если модель <A; Ј > является решёточно-упорядоченным множеством, то алгебра <A; Ъ, Щ >, где операции определены следующим образом: x Ъ y = sup(x,y) и x Щ y = inf(x,y) – решётка.
Заметим, однако, что для гомоморфизмов и подсистем решёток и частично упорядоченных-множеств данное соответствие не сохраняется. Действительно, подалгеброй любой решётки снова является решётка, а подмоделью решёточно-упорядоченного множества не обязательно является решёточно-упорядоченное множество.
Пример 12 (подсистемы ч.у.м. и решеток).
Для решёточно-упорядоченного множества <{1,2,3,6}; | >, где | – отношение делимости, модель <{1,2,3}; | > является подмоделью, однако <{1,2,3}; НОК, НОД > не является подрешёткой решётки <{1,2,3,6}; НОК, НОД >. Действительно, <{1,2,3}; НОК, НОД > – вообще не алгебра, т.к. НОК (наименьшее общее кратное) не является алгебраической операцией на множестве {1,2,3}.
Определение 17 (Дистрибутивная решётка). Решётка <A; Ъ, Щ >, в которой операции Ъ и Щ дистрибутивны одна относительно другой, т.е. для любых элементов a, b, c О A выполняются следующие тождества:
Определение 18 (Нуль, единица). Элемент x О A называется нулём решётки <A; Ъ, Щ >, если для любого элемента a О A выполняется тождество
Предложение 2 (Единственность нуля и единицы). Нуль и единица единственны (если существуют).
Доказательство. Докажем единственность нуля (аналогично доказывается единственность единицы). Пусть x и y – нули. Тогда x Ъ a = a для любого элемента a О A и y Ъ a = a для любого элемента a О A. x Ъ y = y, y Ъ x = x, но x Ъ y = y Ъ x, значит x = y.
В силу данного утверждения мы можем обозначать нуль и единицу специальными символами, а именно: 0 и 1.
Предложение 3 (Свойства нуля и единицы). Для любого элемента a О A выполняются тождества
Доказательство. Докажем тождество 0 Щ a = 0 (тождество 1 Ъ a = 1 доказывается аналогично). 0 Щ a = 0 Щ (0 Ъ a). А 0 Щ (0 Ъ a) по закону поглощения равно 0.
Определение 19 (Дополнение). Элемент a' называется дополнением элемента a в решётке <A; Ъ, Щ >, если a Ъ a' = 1, a Щ a' = 0.
Определение 20 (Решётка с дополнением). Решётка <A; Ъ, Щ >, в которой для каждого элемента a О A существует дополнение a' О A, называется решёткой с дополнением.
Определение 21 (Булева решётка). Дистрибутивная решётка с дополнением называется булевой решёткой.
Рассмотрим все подалгебры некоторой алгебры с конечным носителем и операции: пересечение двух подалгебр и нахождение минимальной алгебры, содержащей две данные алгебры. В общем случае такой объект не является решёткой, так как пересечение двух подалгебр может быть пусто. Но если к подалгебрам мы добавим пустое множество, получим решетку. Покажем это.
Определение 22 (Булева алгебра). Булевой алгеброй называется алгебраическая система <B; +, ·, ¬, 0, 1 &